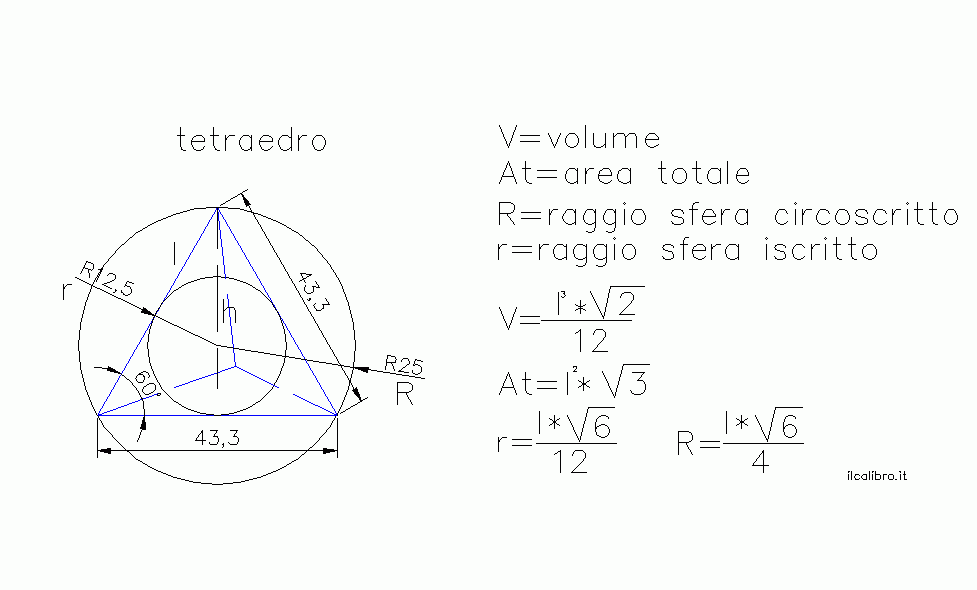
area, volume, raggio sfera iscritto e circoscritto
Il più semplice dei poliedri, che ha 4 vertici, 6 spigoli, 4 facce triangolari e può essere pensato come una piramide a base triangolare.
Le mediane di un t. (ossia i segmenti che congiungono ciascun vertice con il baricentro della faccia opposta) s’incontrano in uno stesso punto, il baricentro del t., che divide ogni mediana in due parti, delle quali quella che
contiene il vertice è tripla dell’altra. Le rette che passano per il centro del cerchio circoscritto a ogni
faccia e che sono perpendicolari alla faccia stessa s’incontrano anch’esse in uno stesso punto,
detto circocentro del t., che è il centro della sfera circoscritta al tetraedro. I 6 piani bisettori dei diedri del t. si incontrano anch’essi in uno stesso punto, l’incentro , che è il
centro della sfera interna al t. e tangente a tutte le facce.
Diversamente da quanto avviene nei triangoli, le altezze di un t., ossia le rette per ciascun vertice
perpendicolari alla faccia opposta, non si incontrano in uno stesso punto; ciò
avviene solo per i t. ortocentrici.
Dal gr. tetráedron, comp.di tétra- "tetra" e hédra "base, faccia"
GB=Tetrahedron F=Tétraèdre D=Tetraeder E=Tetraedro
Info su questa figura
QUI